Archive for April 2016

TRIK PERKALIAN TERCEPAT DAN RUMUS KUADRAT TANPA KALKULATOR

Add Comment
Matematika itu sangat mudah. Seperti kita ketahui matematika adalah salah satu pelajaran yang sangat tidak disukai dan dibenci oleh banyak sekali orang karena rumus dari matematika yang sangat rumit yang membuat orang membenci pelajaran tersebut. Sebenarnya banyak cara mudah dan cepat yang biasa saya berikan kepada murid-murid saya yang sering dikenal sebagai cara Mental Sum yang menjadi value added Bimbel Akong.

 Cara mental sum ini sebenarnya sudah diperkenalkan secara dini untuk murid murid bersekolah SD (primary) bahkan Playgroup di Singapore, dimana mereka tidak diperbolehkan berhitung menulis, namun dipikirkan di otak, kemudian setelah beberapa detik ditulis jawabannya. Ketika saya business travel di Singapore, anak TK B di Singapore ternyata sudah belajar perkalian dua digit, tanpa menghitung manual, namun dipikir di otak. Bagaimana dengan di Indonesia?

Saya akan share sedikit deh, 9 cara mudah berhitung matematika berikut ini

1. Rumus Kuadrat dua digit dengan awalan digit lima

Cara menghitungnya adalah dengan menambahkan bilangan 25 dengan satuan bilangan yang akan dikuadratkan. Kemudian kuadratkanlah satuan bilangan yang akan dikuadratkan tersebut. Lalu gabungkan (Khusus untuk angka satuan 1,2, dan 3 hasil kuadratnya harus dituliskan dengan 01, 04, dan 09)

Contohnya

Berapa Kuadrat 56 = ?

25 + 6 (6 merupakan digit terakhir)  = 31
Kuadrat 6 = 36
Hasil gabungan akhirnya adalah 3136
2. Rumus Kuadrat tiga digit dengan digit akhir lima

Firstly, kalikan angka sebelum angka lima dengan angka urutan selanjutnya dan kemudian tuliskan angka 25 di belakang dengan angka dari hasil pertama

Contohnya:

Berapa Kuadrat 225 = ?

Angka sebelum 5, yakni angka 22. Kemudian, angka setelah 22 yakni angka 23. Kemudian kita kalikan 22 x 23 = 506
Kemudian hasilnya kita tambahkan angka 25 di belakangnya, sehingga hasilnya adalah 50.625
3.Rumus kuadrat dua digit dengan digit terakhir satu

Ambil angka puluhan kemudian dikuadratkan (misalkan diperoleh C). Kemudian ambil kembali angka puluhan yang pertama (misalkan A), kemudian dapatkan 1 angka setelah angka puluhan tersebut (misalkan B). Lalu tambahkan A dan B, semisal diperoleh D. Akhirnya tambahkan C+D

Contohnya:

Berapa Kuadrat 31 = ?

Kuadrat 30 = 900 …. (C)
Angka setelah 30 (A), yakni 31 (B)
31 + 30 = 61 …. (D)
Jumlahkan C+D   = 900 + 61 = 961
4.Rumus perkalian satu digit atau dua digit dengan 99

Mula-mula kurangi bilangan pertama dengan angka 1 terlebih dahulu kemudian kurangi bilangan 100 dengan bilangan tersebut. Hasil akhirnya tinggal digabungkan saja.

Contohnya :

Berapa 42 x 99 = ?

42 – 1 = 41
100 – 42 = 58
Hasilnya adalah 4158
5.Rumus perkalian dua digit dengan angka 11

Perhitungan ini seperti membalikkan telapak tangan. Mula-mula untuk bilangan pertama (selain 11), kita sisipkan dua digit tersebut, dengan 1 digit yang merupakan hasil penjumlahan kedua digit bilangan bersebut.

Contohnya:

Berapa 72 x 11 = ?

7 ? 2
7 + 2 = 9
Hasilnya adalah 792
6.Rumus perkalian dua digit dengan 101

Piece of pizza, yakni dengan cara tuliskan angkanya dua kali.

Contohnya adalah

Berapa 33 x 101 = ?

33ditulis 2 kali sehingga menjadi 3333
7.Rumus perkalian even number dengan 1,5 atau 2,5 atau 3,5 dan seterusnya

Kalikan bilangan pengalian dengan 2. Lalu bilangan pertama yang dikalikan dibagi dengan angka 2. Hasil akhirnya adalah perkalian dari bilangan pengalian dengan 2 dengan hasil dari bilangan yang dibagikan dengan angka 2

Contoh 1 :

Berapa 32 x 2,5 = ?

2,5 x 2 = 5
32 : 2 = 16
Hasilnya adalah 5 x 16 = 80
Contoh 2 :

Berapa 20 x 7,5 = ?

7,5 x 2 = 15
20 : 2 = 10
Hasilnya adalah 15x 10 = 150
8.Rumus perkalian dua bilangan (dua digit) dengan nilai berselisih dua

Pertama tama adalah kuadratkan bilangan di antaranya. Lalu hasilnya dikurangkan dengan 1

Contohnya:

Berapa 14 x 16 = ?

Kuadrat 15 = 225
Hasilnya adalah 225 – 1 = 224
9. Rumus perkalian dua bilangan dengan digit puluhan kedua bilangan yang bernilai sama dan jumlah digit kedua bilangan satuannya adalah 10

Mula mula kalikan bilangan puluhan dengan bilangan berikutnya , lalu kalikan masing-masing digit satuannya. Hasil akhirnya adalah penggabungan hasil dari bilangan puluhan yang di kalikan dengan bilangan satuan yang di kalikan.

Contohnya:

Berapa 38 x 32 = ?

3 x 4 = 12
8 x 2= 16
Hasilnya adalah 1216
Ternyata sangat mudah kan untuk mengerjakan perkalian dan kuadrat dengan rumus ini.

Rumus Percepatan Dalam Fisika

Add Comment
Dalam fisika, percepatan atau akselerasi adalah perubahan kecepatan dalam satuan waktu tertentu. Umumnya, percepatan dilihat sebagai gerakan suatu objek yang semakin cepat ataupun lambat. Namun percepatan adalah besaran vektor, sehingga percepatan memiliki besaran dan arah. Dengan kata lain, objek yang membelok (misalnya mobil yang sedang menikung)-pun memiliki percepatan juga.
Satuan SI percepatan adalah m/s2. Dimensi percepatan adalah L T−2.
Percepatan (dilambangkan dengan a) mengikuti rumus sebagai berikut:
\begin{alignat}{3} \mathbf{a} & = \frac{d \mathbf{v}}{dt} \\ & = \frac{\mathrm{d}v }{\mathrm{d}t} \mathbf{u}_\mathrm{t} +v(t)\frac{d \mathbf{u}_\mathrm{t}}{dt} \\ & = \frac{\mathrm{d}v }{\mathrm{d}t} \mathbf{u}_\mathrm{t}+ \frac{v^2}{R}\mathbf{u}_\mathrm{n}\ \\ \end{alignat}
Dalam mekanika klasik, percepatan suatu objek bermassa tetap berbanding lurus dengan resultan gaya yang bekerja padanya dan berbanding terbalik dengan massanya.
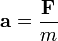
\mathbf{a} = \frac{\mathbf{F}}{m}
Percepatan bisa bernilai positif dan negatif. Bila nilai percepatan positif, hal ini menunjukkan bahwa kecepatan benda yang mengalami percepatan positif ini bertambah (dipercepat). Sebaliknya bila negatif, hal ini menunjukkan bahwa kecepatan benda menurun (diperlambat). Contoh percepatan positif adalah: jatuhnya buah dari pohonnya yang dipengaruhi oleh gravitasi. Sedangkan contoh percepatan negatif adalah: proses pengereman mobil.

Contoh Soal :

Sebuah mobil mempunyai massa 3.000 kg. Dari keadaan diam mulai bergerak setelah 12 sekon kecepatan mobil mencapai 6 m/s. Hitunglah gaya yang bekerja pada mobil !

Penyelesaian:
Diketahui    :    m  = 3 000 kg
                        vo = 0 m/s 
                        vt = 6  m/s
                        t   = 12 s

Ditanyakan :     F  = …… ?

Jawab         :      Mencari percepatan (a)

            ∆v
a =  ---------             
            Δt

       (6 – 0) m/s
a = ---------------              
       (12 – 0) s

a = 0,5 m/s2
Mencari gaya (F)
F = m . a
F = 3 000 kg . 0,5 m/s2
F = 1 500 N

Jadi gaya yang bekerja pada mobil adalah 1 500 N

Rumus Luas Lingkaran dan Rumus Keliling Lingkaran

Add Comment
Istilah geometri mengenai lingkaran, yaitu :
  • Istilah yang menunjukkan titik, yaitu :
    1. Titik pusat (P)
      merupakan titik tengah lingkaran, di mana jarak titik tersebut dengan titik manapun pada lingkaran selalu tetap.
  • Istilah yang menunjukkan garisan, yaitu :
    1. Jari-jari (R)
      merupakan garis lurus yang menghubungkan titik pusat dengan lingkaran.
    2. Tali busur (TB)
      merupakan garis lurus di dalam lingkaran yang memotong lingkaran pada dua titik yang berbeda.
    3. Busur (B)
      merupakan garis lengkung baik terbuka, maupun tertutup yang berimpit dengan lingkaran.
    4. Keliling lingkaran (K)
      merupakan busur terpanjang pada lingkaran.
    5. Diameter (D)
      merupakan tali busur terbesar yang panjangnya adalah dua kali dari jari-jarinya. Diameter ini membagi lingkaran sama luas.
    6. Apotema
      merupakan garis terpendek antara tali busur dan pusat lingkaran.
  • Istilah yang menunjukkan luasan, yaitu :
    1. Juring (J)
      merupakan daerah pada lingkaran yang dibatasi oleh busur dan dua buah jari-jari yang berada pada kedua ujungnya.
    2. Tembereng (T)
      merupakan daerah pada lingkaran yang dibatasi oleh sebuah busur dengan tali busurnya.
    3. Cakram (C)
      merupakan semua daerah yang berada di dalam lingkaran. Luasnya yaitu jari-jari kuadrat dikalikan dengan pi. Cakram merupakan juring terbesar.

Persamaan

Suatu lingkaran memiliki persamaan
(x - x_0)^2 + (y - y_0)^2 = R^2 \!
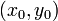dengan R\! adalah jari-jari lingkaran dan (x_0,y_0)\! adalah koordinat pusat lingkaran.
Jika pusat lingkaran terdapat di (0,0) \!, maka persamaan di atas dapat dituliskan sebagai
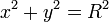
x^2 + y^2 = R^2 \!
Bentuk persamaan lingkaran dapat dijabarkan juga menjadi bentuk
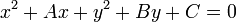
x^2 + Ax + y^2 + By + C = 0 \!
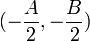dengan \sqrt{\frac{A^2 + B^2}{4} - C} \! adalah jari-jari lingkaran dan (- \frac{A}{2}, -\frac{B}{2}) \! adalah koordinat pusat lingkaran. Bentuk persamaan tersebut dikenal sebagai bentuk umum persamaan lingkaran.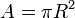

Luas lingkaran

Luas lingkaran memiliki rumus
A = \pi R^2 \!
yang dapat diturunkan dengan melakukan integrasi elemen luas suatu lingkaran
dA = rd\theta\ dr
dalam koordinat polar, yaitu
\int dA = \int_{r=0}^R \int_{\theta=0}^{2\pi} rd\theta\ dr = \int_{r=0}^R rdr \int_{\theta=0}^{2\pi} d\theta = \frac 1 2 (R^2-0^2) \ (2\pi-0) = \pi R^2 \!
Dengan cara yang sama dapat pula dihitung luas setengah lingkaran, seperempat lingkaran, dan bagian-bagian lingkaran. Juga tidak ketinggalan dapat dihitung luas suatu cincin lingkaran dengan jari-jari dalam R_1\! dan jari-jari luar R_2\!.
contoh soal:
1. jika diketahui sebuah roda mainan mempunyai diameter 14 cm. Tentukan luas lingkaran roda tersebut!
Jawab:
d = 14 cm
karena d = 2 x r maka:
r = d/2
r = 14/2
r = 7 cm
Luas = π x r2
Luas = 22/7 x 72
Luas = 154 cm2
2. hitunglah luas lingkaran yang memiliki jari-jari 10 cm!
Jawab:
r = 10 cm
Luas = π x r2
Luas = 3,14 x 102
Luas = 314 cm2

Keliling lingkaran

Keliling lingkaran memiliki rumus:
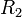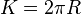
K = 2\pi R\!

Panjang busur lingkaran

Panjang busur suatu lingkaran dapat dihitung dengan menggunakan rumus
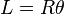
L = R \theta \!
yang diturunkan dari rumus untuk menghitung panjang suatu kurva
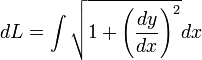
dL = \int \sqrt{1 + \left( \frac{dy}{dx}\right) ^2 } dx \!
di mana digunakan
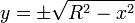
y = \pm \sqrt{R^2 - x^2} \!
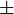sebagai kurva yang membentuk lingkaran. Tanda \pm mengisyaratkan bahwa terdapat dua buah kurva, yaitu bagian atas dan bagian bawah. Keduanya identik (ingat definisi lingkaran), sehingga sebenarnya hanya perlu dihitung sekali dan hasilnya dikalikan dua.
contoh soal:
2. hitunglah keliling lingkaran yang memiliki diameter 20 cm!
Jawab:
d = 20 cm
Π  = 3,14
Keliling  = π x d
Keliling  = 3,14 x 20
Keliling  = 62,8 cm

Rumus Dan Estimasi Waktu Penyelesian Proyek

Add Comment

Estimasi Waktu Penyelesian Proyek

-       Ditentukan oleh tim proyek berdasarkan konsensus bersama antar anggota tim atau pengalaman proyek sejenis
-       Dua pendekatan estimasi:


(a)     Menggunakan 3 nilai : Optimistik (a), Umum (m), dan 
         Pesimistik (b)            PERT


Te = (a + 4m + b)/ 6     

Dimana:    Te = Taksiran waktu
                      V = variansi



V = ((b-a )/ 6)2  untuk 0 dan 100%

                     Atau

V = ((b-a) / 3,2) 2  untuk 5% (tingkat kepercayaan 95%)


            Contoh:

Kode aktivitas
Aktivitas pendahulu
Taksiran waktu penyelesaian (bln)
Optimistik
       (a)
Umum
   (m)
Pesimistik
    (b)
Te
A
B
C
D
E
F
G
H
I
J
K
L
-
-
-
A
A
B
C
D
B,G
H
E,F
I
1
2
3
2
2
1
1
1
4
1
5
1
2
3
4
4
3
3
4
3
4
3
7
      1
3
4
5
6
10
5
7
11
4
11
15
1
2
3
4
4
4
3
4
4
4
4
8
1





3.  Mengidentifikasi Jalur Kritis

Lintasan Kritis  = Max. V


Contoh:

Kode aktivitas
Aktivitas pendahulu
Taksiran waktu penyelesaian (bln)
Optimistik
       (a)
Umum
   (m)
Pesimistik
    (b)
Te
 V
A
B
C
D
E
F
G
H
I
J
K
L
-
-
-
A
A
B
C
D
B,G
H
E,F
             I
1
2
3
2
2
1
1
1
4
1
5
       1
2
3
4
4
3
3
4
3
4
3
7
    1
3
4
5
6
10
5
7
11
4
11
15
        1
2
3
4
4
4
3
4
4
4
4
8
    1
0,39
0,39
0,39
1,56
6,25
1,56
3,52
9,77
-
9,77
9,77
-
           

Lintasan kritis:

1. A-D-H-J ;   VADHJ = VA + VD + VH + VJ
                                    = 0,39 + 1,56 + 9,77 + 9,77
                                    = 21,49          

2. A-E-K;        VAEK  = VA + VE+ VK
                                    =  0,39 + 6,25 + 9,77
                                    = 16,41

3.B-F-K;          VBFK = VB + VF + VK
                                    = 0,39 + 1,56 + 9,77
                                    = 11,72


Lintasan kritis adalah ADHJ karena nilai V-nya paling besar





(b)  menggunakan 1 nilai waktu, digunakan untuk proyek yang sudah ada waktu rata-rata (waktu baku)             CPM




4.  Menganalisis jadual penyelesaian proyek


Notasi Yang Digunakan:

TE = Saat tercepat terjadinya event
TL = Saat paling lambat terjadinya event
ES = Saat tercepat dimulainya aktivitas
EF = Saat tercepat selesainya aktivitas
LS = Saat paling lambat dimulainya aktivitas
LF = Saat paling lambat diselesaikannya aktivitas
  t  = waktu yang diperlukan untuk sutau aktivitas hari/waktu) 
  S = Total slack/total float
SF = Free slack/free float


Asumsi Yang Berlaku

  1. Proyek hanya memiliki satu initial event dan satu terminal event
  2. Saat tercepat terjadninya initial event adalah hari ke nol
  3. Saat paling lambat terjadinya terminal event adala TL=TE untuk event ini.


Lingkaran kejadian (event) dibagi atas 3 bagian:





 Cara Perhitungan
(1)  Perhitungan Maju
-       Saat tercepat terjadinya initial event ditentukan pada hari ke nol, sehingga berlaku TE = 0, kecuali jika proyek dependent terhadap proyek lain.
-       Jika initial event terjadi pada hari ke nol, maka:
ES (i,j) = TE (j) = 0
EF (i,j) = ES (i,j) + t (i,j)
             = TE (i) + t (i,j)



 

Sebuah event hanya dapat terjadi jika aktivitas-aktivitas yang mendahuluinya telah selesai, maka saat peling cepat terjadinya sebuah event sama dengan nilai terbesar dari saat tercepat untuk menyelesaikan aktivitas-aktivitas yang berakhir pada event tersebut.

            TE = max [EF(i1,j), EF(i2,j),....., EF (in,j)]



(2) Perhitungan Mundur
-       Pada terminal event berlaku TL = TE
-       Saat paling lambat untuk memulai suatu aktivitas sama dengan saat paling lambat untuk menyelesaikan aktivitas itu dikurangi dengan waktu aktivitas tersebut



 






 



   Saat paling lambat terajadinya sebuah event sama dengan nilai terkecil dari saat-saat paling lambat untuk memulau aktivitas-aktivitas yang bermula dari event tersebut.


            TL(i) = min [(LS (i,j1) , LS (i,j2), ......, LS (i,jn)]  
Langganan: Postingan (Atom)